
QAM symbols are represented by the carrier signal being transmitted with specific phase (90°)/amplitude (dictated by the message), for finite periods of time.
QAM constellations (patterns)
2 QAM (Binary PSK – BPSK)
Two symbols are defined (1 amplitude; 2 phases)
Every symbol transmitted over the transmission channel represents (carries) 1 message bit.
Baud rate = bit rate
QAM is a modulation method modifying the phase and the amplitude of the carrier signal. QAM symbols are represented by the carrier signal being transmitted with specific phase / amplitude (dictated by the message), for finite periods of time.
One symbol is identified by a Q and an I (Inphase) value. Transmission channels with a limited bandwidth limit the amount of symbols per second (Baud rate) that can be transmitted To increase the bit per sec (bps) capacity of a channel, while keeping the Baud rate at the low values imposed by the channel bandwidth, the symbols carry (represent) more than one single bit.
Symbols will represent a number of n bits, increasing the channel capacity by a factor of n The price paid is the presence of multiple symbols in the channel, increasing the probability of incorrect symbol identification at the receiver
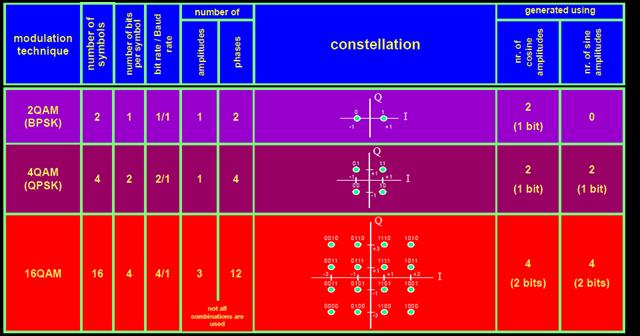
More complex modulation techniques transmit more bits within one symbol. This means the radio link has to differentiate between a higher number of symbols.
- 4 symbols: 2 bits are represented by one symbol
- 16 symbols: 4 bits are represented by one symbol
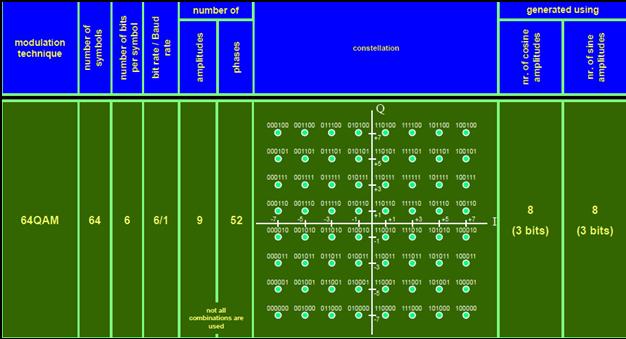
The figure shows the highest modulation scheme (64 QAM) used by the WiMAX physical layer. The radio link has to differentiate between 64 symbols ( 8 values in I and Q-direction). The effect of noise in a channel leads to produce uncertainty in the position of the symbols in the I/Qconstellation. If the demodulator detects the phase state closest to the wrong point in the constellation, then a symbol error – and consequently bit errors occur.
As the spectrum occupancy is proportional to the symbol rate, systems using more phase states are more spectrum efficient.